Вычитаем столбиком с примерами на картинках

Признаки делимости величин

Перед использованием признаков делимости чисел нужно понимать, что величины классифицируются на простые и составные. Первые делятся только на 1 и эквивалентное себе значение. Вторые могут содержать нескольких множителей. В последнем случае и необходимо использовать правила деления.

Следует отметить, что для удобства специалисты рекомендуют составить письменную карточку с таблицей простых величин или распечатать ее при помощи принтера, предварительно загрузив из интернета. Правила делимости многозначного на однозначное число имеют следующий вид (делители соответствуют порядковому номеру списка):

Любое значение, т. е. 34/1=34.
Величина, заканчивающаяся четной цифрой.
Сумма цифр разрядной сетки должна делиться на тройку.
Сумма двух последних элементов делится на четверку.
Величина заканчивается на ноль или пятерку.
Сумма цифр делится на тройку, а также число является четным.
Число разбивается на разряды по три элемента (без последних), которые суммируются между собой. Она должна делиться на 7. Если величина имеет небольшое количество знаков (двузначная, трехзначная, четырехзначная или пятизначная), то нужно взять числа без последнего компонента разрядной сетки. Затем от них отнять удвоенное значение разряда единиц. Результат разности должен делиться на 7. Например, 259/7 -> 25−2*9=25−18=7 (делится).
Если выполняется условие для 2 и 4 одновременно.
Сумма компонентов разрядной сетки делится на девятку.
Величина заканчивается 0.

Следует отметить, что реализация правила деления величины 45134412 на семерку выполняется следующим образом: | 45 | 134 | 412 =9+8+7=24 — не делится на 7. Применить способ для малого количества разрядов не получится, поскольку на вычисления будет затрачено много времени.

Как правильно делить в столбик?

Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).

Как найти частное двух чисел – 35 и 5?

1. Пишем числа, участвующие в делении, так:
   Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное.
2. Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
3. Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.
4. Проверяем правильность действий путем умножения: 7 X 5=35. Все верно, решение выполнено точно.

Работа с многозначными числами

Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:

1. Определяем делимое (372) и делитель (6), оформляем запись в уголок:
2. Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
3. Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
4. Вычитаем из 37-36=1. Пишем единичку слева внизу под чертой:
5. В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:

Пример решен, можно проверить правильность путем умножения: 62X6=372.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Как посчитать сумму в столбце за исключением заголовка или исключая несколько первых строк

Обычно ссылки на столбцы используются в формуле СУММ для того, чтобы посчитать сумму в столбце, игнорируя заголовок, как показано на приведенном выше изображении. Но в некоторых случаях заголовок столбца может содержать какое-то числовое значение. Или, например, вы хотите исключить первые несколько строк с числами, которые не имеют отношения к данным.

К сожалению, Microsoft Excel не принимает смешанную формулу СУММ с явной нижней границей, но без верхней границы, например, такой как =СУММ(B2: B). Если вам необходимо посчитать сумму в столбце, исключив первые несколько строк, вы можете использовать одно из следующих нескольких решений.

1. Посчитайте сумму столбца, а затем вычтите ячейки, которые вы не хотите включать в общую сумму (ячейки B1-B3 в данном примере):

Урок вычитание

Вычитание – это арифметическое действие, в процессе которого ищется разность 2 чисел и ответов является третье.Формула сложения выражается так: a — b = c
.

Примеры и задачи Вы сможете найти ниже.

При вычитании дробей
следует помнить, что:

Дана дробь 7/4, получаем, что 7 больше 4, а значит 7/4 больше 1. Как выделить целую часть? (4+3)/4, далее получаем сумму дробей 4/4 + 3/4, 4:4 + 3/4=1 + 3/4. Итог: одна целая, три четвертых.

Вычитание 1 класс

Первый класс – начало пути, начало обучения и изучения основ, в том числе и вычитания. Обучение стоит вести в игровой форме. Всегда в первом классе вычисления начинают с простых примеров на яблоках, конфетах, грушах. Используется этот метод не зря, а потому что детям намного интереснее, когда с ними играют. И это не единственная причина. Яблоки, конфеты и тому подобное дети видели очень часто в свой жизни и имели дело с передачей и количеством, поэтому научить сложению таких вещей будет не сложно.

Задачи на вычитание первоклассникам можно придумать целую тучу, к примеру:

Задача 1.
Утром, гуляя по лесу ежик нашел 4 грибочка, а вечером, когда пришел домой, ежик на ужин скушал 2 грибочка. Сколько грибочков осталось?

Задача 2.
Маша пошла в магазин за хлебом. Мама дала маше 10 рублей, а хлеб стоит 7 рублей. Сколько Маша должна принести денег домой?

Задача 3.
В магазине утром на прилавке находилось 7 килограмм сыра. До обеда посетители выкупили 5 килограмм. Сколько килограмм осталось?

Задача 4.
Рома вынес во двор конфеты, который дал ему папа. У Ромы было 9 конфет, а своему другу Никите он дал 4. Сколько конфет осталось у Ромы?

Первоклассники в основном решают задачи, в которых ответом будет число от 1 до 10.

Вычитание 2 класс

Второй класс это уже выше первого, а соответственно и примеры для решения тоже. Итак, приступим:

Числовые задания:

Однозначные числа:

1. 10 — 5 =
2. 7 — 2 =
3. 8 — 6 =
4. 9 — 1 =
5. 9 — 3 — 4 =
6. 8 — 2 — 3 =
7. 9 — 9 — 0 =
8. 4 — 1 — 3 =

Двузначные числа:

1. 10 — 10 =
2. 17 — 12 =
3. 19 — 7 =
4. 15 — 8 =
5. 13 — 7 =
6. 64 — 37 =
7. 55 — 53 =
8. 43 — 12 =
9. 34 — 25 =
10. 51 — 17 — 18 =
11. 47 — 12 — 19 =
12. 31 — 19 — 2 =
13. 99 — 55 — 33 =

Текстовые задачи

Вычитание 3-4 класс

Суть вычитания в 3-4 классе – вычитание в столбик больших чисел.

Рассмотрим пример 4312-901. Для начала запишем числа друг под другом, так чтобы из числа 901 единица была под 2, 0 под 1, 9 под 3.

Затем производим вычитание справа налево, то есть из числа 2 число 1. Получаем единицу:

Вычитая из тройки девять, нужно позаимствовать 1 десяток. То есть из 4 вычитаем 1 десяток. 10+3-9=4.

А так как у 4 заняли 1, то 4-1=3

Ответ: 3411.

Вычитание 5 класс

Пятый класс – это время для работы над сложными дробями с разными знаменателями. Повторим правила:1. Вычитаются числители, а не знаменатели.

Итак, вычитаем. Убедились, что знаменатели одинаковые. Тогда вычитаем числители (2-1)/4, так получаем 1/4. При складывании дробей, вычитаются только числители!

2. Чтобы осуществить вычитание, убедитесь, что знаменатели равны.

Попалась разность дробей, к примеру, 1/2 и 1/3, то домножить придется не одну дробь, а обе, чтобы привести к общему знаменателю. Самый простой способ сделать это: первую дробь умножить на знаменатель второй, а вторую дробь на знаменатель первой, получаем: 3/6 и 2/6. Складываем (3-2)/6 и получаем 1/6.

3. Сокращение дроби производится путем деления числителя и знаменателя на одинаковое число.

Дробь 2/4 можно привести к виду ½. Почему? Что из себя представляет дробь? ½ = 1:2, а если делить 2 на 4, то это тоже самое, что делить 1 на 2. Поэтому дробь 2/4 = 1/2.

4. Если дробь больше единицы, то можно выделить целую часть.

Дана дробь 7/4, получаем, что 7 больше 4, а значит 7/4 больше 1. Как выделить целую часть? (4+3)/4, далее получаем сумму дробей 4/4 + 3/4, 4:4 + 3/4=1 + 3/4. Итог: одна целая, три четвертых.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Вычитание столбиком

Для того, чтобы вычесть столбиком два числа, нужно сначала правильно их записать. Два числа записываются друг под другом, так чтобы каждое число соответствовало своему разряду. То есть единицы записываются под единицами, десятки под десятками и так далее.

Если у числа имеется десятичная дробная часть, то она записывается по тому же принципу: десятые под десятыми, сотые под сотыми и так далее. Если вдруг получилось, что у одного числа есть сотые, а у другого их нет, то нужно просто во втором числе дописать нули для удобства вычисления. Два числа подчеркиваются, и под чертой пишется результат вычисления.

Сам процесс вычитания прост: из единиц уменьшаемого вычитаются единицы вычитаемого и так далее. То есть все вычитание разбивается на много вычитаний маленьких чисел не больше 9.

Приведем пример:

19590-13587

• Вычитаем единицы: 0-7 – вычесть единицы не получится, значит нужно единицу у следующего разряда. Значит, в следующем действии мы будем вычитать не из 9, а из 8. При этом 1 следующего разряда это 10 для настоящего. То есть, пример превращается в: 10-7=3
• По тому же принципу выполняем оставшиеся действия: 8-8=0
• 5-5=0
• 9-3=6
• 1-1=0 – десятков тысяч в записи не будет, так как получился ноль.
• Следующий шаг это правильная запись ответа, но при решении столбиком ответ получится сам собой: 6033

19590-13587=6033

Особое внимание нужно обращать на «займы» у следующих разрядов. В математике эта операция имеет название вычитания в столбик с переходом через десяток

Нужно понимать, что вычитая единицы, мы забрали 1 у разряда десятков. А 1 десяток это сколько 1? Верно, десять, так же как в 1 сотне 10 десятков и так далее. Понимание этого факта есть залог успешного вычитания.

Иногда ученикам начинает казаться, что вычитание столбиком не нужно, ведь давно изобретен калькулятор. Однако, когда мозг выполняет больше вычисления, он обретает навык, расширяя нейронные связи, что хорошо сказывается на дальнейшем обучении любой специальности. К тому же, в ближайшее время на экзаменах по математике вряд ли разрешать пользоваться калькулятором, поэтому стоит учиться правильно вычитать как можно раньше, так как это избавит вас от лишних забот в будущем.

Что мы узнали?

Мы поговорили о том, что такое вычитание и какие результаты могут получаться в результате этой операции. Отдельно выделили вычитание столбиком и рассмотрели его на небольшом примере. Особенно остановились на переходе через десяток, как на наиболее сложном моменте вычитания.

1. Вопрос 1 из 10

Начать тест(новая вкладка)

Вычитание столбиком подробное описание

Располагаем наши два числа, которые должны вычесть столбцом, по правилам, правая цифра под правой цифрой:

Смотрим первый столбец справа — 5 минус 4 — стандартная операция вычитания из большего числа меньшее, равно 1.

Второй столбец — 4 минус 9. 4 меньше 9, поэтому, забираем десяток из соседнего левого столбца(3) там остается 2.

Оставляем зарубку ‘ над числом 3, чтобы не забыть, что мы взяли оттуда единицу!

К десяти прибавляем 4 = 14, теперь мы можем отнять от 14 цифру 9 = 5 — сносим под черту.

Переходим к третьему столбцу справа. Это 3, но мы поставили там зарубку, что мы отсюда забрали единицу, значит здесь у нас осталась только двойка, 2 -1 = 1, сносим единицу под черту.

И последний столбец, под цифрой 8 ничего нет, и мы у восьмерки ничего не занимали, поэтому сносим её под черту без изменений.

Калькулятор вычитания столбиком

Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить .

Существует удобный метод нахождения разности двух натуральных чисел – вычитание в столбик, или вычитание столбиком. Этот способ берет свое название от метода записи уменьшаемого и разности друг под другом. Так можно провести и основные, и промежуточные вычисления в соответствии с нужными разрядами чисел.

Этим методом удобно пользоваться, поскольку это очень просто, быстро и наглядно. Все сложные на первый взгляд подсчеты можно свести к сложению и вычитанию простых чисел.

Ниже мы рассмотрим, как именно пользоваться этим методом. Наши рассуждения будут подкреплены примерами для большей наглядности.

Использование формулы с помощью параметра «СУММ»

Этот способ особенно хорош тогда, когда вам нужно занести результат в определенную ячейку. По крайней мере я пользуюсь этим именно так и доволен как слон. Давайте покажу.

1. Поставьте курсор в то место, где вы хотите, чтобы отображался ваш результат и поставьте туда уже знакомый нам знак равенства.
2. Теперь нам нужно выполнить функцию «СУММ». Ее вы можете выбрать в левом верхнем углу листа, нажав на него. Либо вы можете увидеть ее во вкладке «Формулы» , а затем выбрать «Математические» , и уже там, среди множества других функций, искать заветную СУММ. В общем жмахайте.
3. Вам откроется окно с аргументами функции. Здесь вы должны будете выбрать диапазон чисел, которые будете складывать. Например я хочу сложить столбик от А1 до А7. Тогда поставьте курсор в графу «Число 1» , а затем выделите нужные ячейки.
4. Теперь нажмите Enter и вы увидите, что всё у вас отлично посчиталось.

Кстати этим же способом вы можете воспользоваться, чтобы посчитать сумму ячеек с разных листов. Давайте расскажу чуть подробнее.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Удобно проводить особым методом, который получил название вычитание столбиком
или вычитание в столбик
. Этот способ вычитания оправдывает свое название, так как уменьшаемое, вычитаемое и разность записываются в столбик. Промежуточные вычисления также проводятся в столбиках, соответствующих разрядам чисел.

Удобство вычитания натуральных чисел столбиком заключается в простоте вычислений. Вычисления сводятся к использованию таблицы сложения и применению свойств вычитания.

Давайте разберемся, как выполняется вычитание столбиком. Процесс вычитания будем рассматривать вместе с решением примеров. Так будет понятнее.

Навигация по странице.

Как научить ребёнка считать до 100

Расскажите ребёнку о том, что десятков всего девять, после этого назовите каждый десяток: десять, двадцать, тридцать и так далее. Предложите ему каждый день заучивать по 10 новых цифр каждого десятка. В конце дня спрашивайте, что ребёнок запомнил и повторяйте то, что он выучил в другие дни. Упростить повторение можно считая предметы, которые находятся перед вами. После того как ребёнок освоит десятки, предложите ему сыграть в игру: напишите ряд чисел с десятками и пропустите одно число в середине, попросив ребёнка вписать в этом месте пропущенное число.

Также можно использовать методику Глена Домана. Сначала ребёнку нужно показывать карточки с количеством точек не более пяти, затем с большим количеством точек — 20, 50 и далее до 100. Этот метод поможет также натренировать зрительную память.

Как посчитать сумму в столбце с помощью функции СУММ

Чтобы посчитать сумму в столбце, вы можете использовать функцию Excel СУММ. Например, чтобы посчитать сумму в столбце B , например, в ячейках B2-B8, введите следующую формулу Excel СУММ:

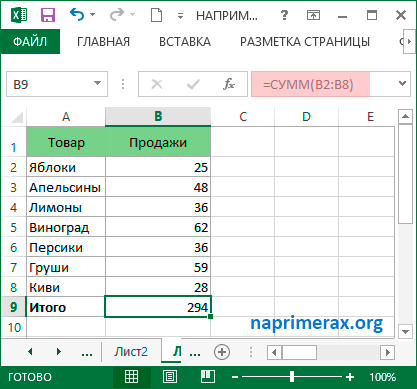
Как посчитать сумму в столбце в Excel – Посчитать сумму в столбце

Существует второй способ, как в Excel посчитать сумму столбца автоматически. Для этого выберите последнюю пустую ячейку в столбце, в котором вы хотите посчитать сумму. На вкладке « ГЛАВНАЯ » в группе « Редактирование », нажмите « Автосумма » и клавишу « Enter ». После этого в ячейке будет автоматически введена формула «СУММ»:

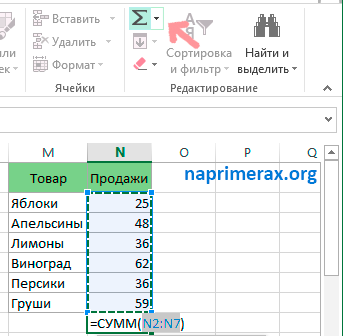
Как посчитать сумму в столбце в Excel – В таблице посчитать сумму столбца с использованием Автосуммы

Сложение многозначных чисел

Многозначные числа складывают по разрядам, используя переместительный и сочетательный законы сложения.

Пример. Сложим двузначные числа  26  и  48:

26 + 48 = (20 + 6) + (40 + 8) = 20 + 6 + 40 + 8 = (20 + 40) + (6 + 8) = 60 + 14 = 60 + (10 + 4) = 60 + 10 + 4 = (60 + 10) + 4 = 70 + 4 = 74.

Сначала мы разложили слагаемые на разряды, затем сгруппировали в одну группу десятки, в другую — единицы и выполнили сложение по разрядам, т. е. сложили десятки с десятками и единицы с единицами, затем один десяток, получившийся от сложения единиц, прибавили к десяткам, которых у нас было 6 от сложения десятков, и в конце сложили десятки с единицами.

Форма записи сложения, которую мы использовали, слишком длинная и потому неудобная, поэтому при сложении многозначных чисел обычно используется другая, более удобная форма записи, которая называется сложением столбиком.

Умножаем и делим, используя таблицу умножения

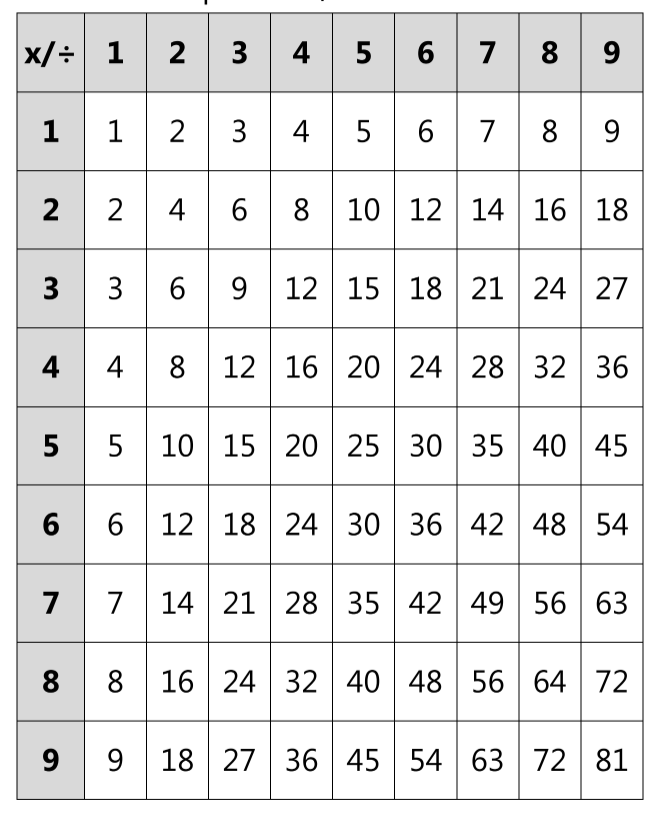
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример:
4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

Вычитание

Вычитание это процесс переноса числа по числовой прямой влево, то есть против движения числовой прямой. При этом результаты вычитания могут быть различны: может получиться ноль, положительное или отрицательное число.

Несмотря на то, что результаты вычисления могут быть различны, результат всегда остается в категории действительных чисел или комплексных чисел, в зависимости от того, какие числа участвовали в вычислении. При вычитании рациональных чисел никогда не получится иррациональное число, а при вычитании действительных – комплексное. Нужно внимательно следить за этим.

Вычитать столбиком можно только рациональные числа с любым знаком. Столбиком не получится подсчитать вычитание обычных дробей, но эта операция всегда представляется в виде вычитания целых чисел в числителе, поэтому таким способом можно вычислять и подобные выражения.

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

Рис. 1

На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.

Методика обучения делению в столбик

Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.

Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.

Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.

Деление в столбик на конкретном примере

Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.

Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.

Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».

Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.

Вот и столбик скоро получится.

Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.

Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9

Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.

Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.

Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.

Снова задают тот же вопрос. Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.

Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.

Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей

Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык

Вычитание чисел

Вычитание чисел легко освоить любому первокласснику. Например, из 6 нужно вычесть 5. 6-5=1, 6 больше числа 5 на единицу, значит, и ответ будет единицей. Можно для проверки произвести сложение 1+5=6. Если вы не знакомы со сложением, то можете прочитать нашу .

Большое число делится на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Если вычитать единицы, то все легко и просто. Но допустим пример: 14-7. В числе 14: 1-десяток, а 4- единицы. 1 десяток – 10 единиц. Тогда получаем 10+4-7, сделаем так: 10-7+4, 10 – 7 =3, а 3+4=7. Ответ найден верно!

Рассмотрим пример 23 -16. Первое число 2 десятка и 3 единицы, а второе 1 десяток и 6 единиц. Представим число 23 как 10+10+3, а 16 как 10+6, тогда представим 23-16 как 10+10+3-10-6. Тогда 10-10=0, останется 10+3-6, 10-6=4, тогда 4+3=7. Ответ найден!

Аналогично делается с сотнями и тысячами

Как посчитать сумму в Excel

• 24 Июль, 2009 –
• Уроки Excel –
• Tags : сумма в excel, таблицы excel
• 76 Comments

Самая простая формула в Excel – это, пожалуй, сумма значений определенных ячеек.

Простейший пример: у вас есть столбец цифр, под ним должна стоять сумма этих цифр.

Выделяете ячейки со значениями, и еще одну пустую под ними, где должно будет расположиться значение суммы. И нажимаем на кнопку автосуммы.

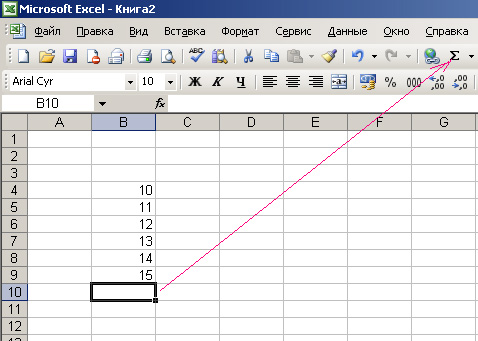
Другой вариант-отмечаем ячейку, где должно быть значение суммы, нажимаем кнопку автосуммы.

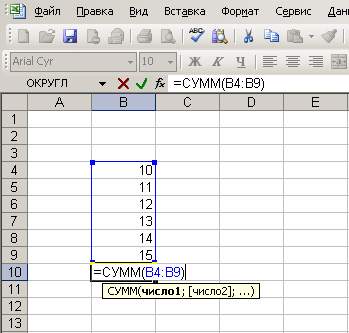
область, значения которой будут просуммированы, выделяется и в ячейки суммы мы видим диапазон просуммированных ячеек. Если диапазон тот, который нужен, просто нажимаем Enter . Диапазон суммирующихся ячеек можно менять

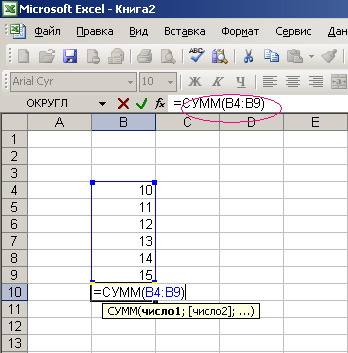
Например B4:B9 можно заменить на B4:B6 см.

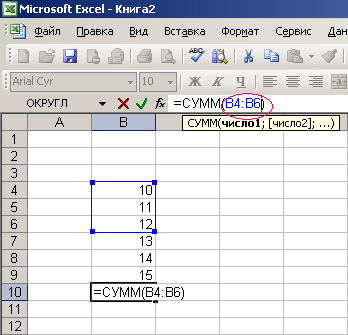
и мы получим результат

Теперь рассмотрим более сложный вариант.

Допустим, нужно сложить значения ячеек, которые не стоят в столбике подряд одно под другим. На рисунке желтым выделены ячейки, значения которых мы будем складывать.

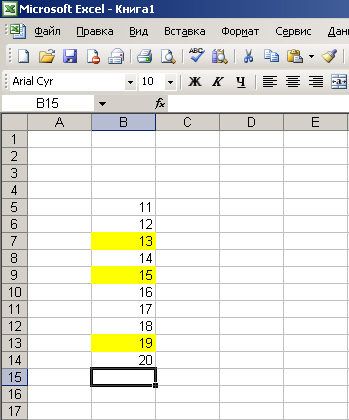
Ставим курсор на той ячейке, где должна быть сумма желтых ячеек. Жмем знак «равно», далее жмем на первую желтую ячейку, и в нашей ячейке суммы начинает формироваться формула. Дальше жмем знак «плюс»(+), за ним жмем на следующую желтую ячейку, затем снова «плюс», и последнюю желтую ячейку, на экране видим следующее:

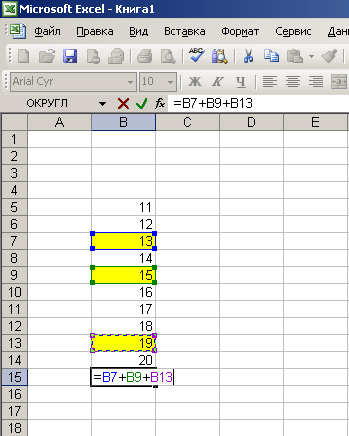
Дальше просто нажимаем Enter и вот мы получили сумму желтых ячеек.

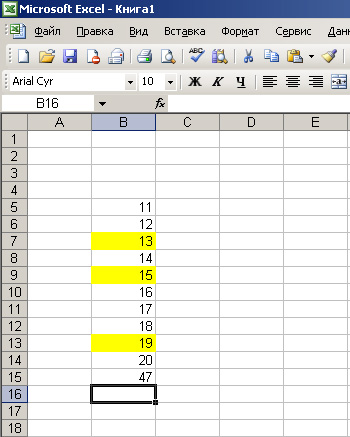
Бывает, что перед Вами не стоит задачи, чтобы в определенной ячейке стояло значение суммы ячеек. Допустим, Вам нужно быстренько посмотреть, какую сумму составляют несколько значений. В Excel и такое возможно

Воспользуемся старым примером с желтыми ячейками.

Внизу листа есть строка состояния. Сейчас там написано «Готово».

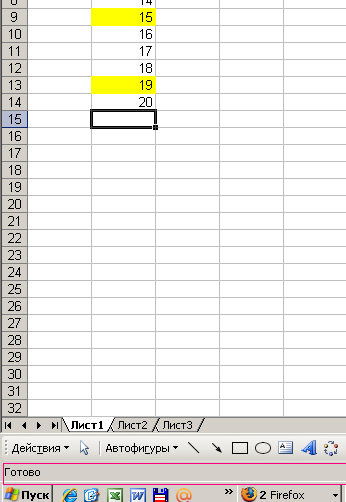
Если нажать правой мышью, появится меню, мы в нем выбираем значение «сумма»

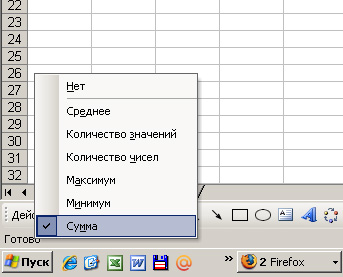
Теперь жмем на первую желтую ячейку, далее нажимаем и удерживаем на клавиатуре кнопку Ctrl и жмем на вторую желтую ячейку, и, продолжая удерживать C trl , жмем на третью желтую ячейку. В итоге мы видим на экране такую картину.

Обратите внимание, в правом нижнем углу появилось значение суммы желтых ячеек