Деление многочлена на многочлен столбиком

Как делить столбиком

Допустим, нам нужно разделить  780  на  12,  записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число  7,  так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число  78  больше делителя, поэтому мы начинаем деление с него:

В нашем случае число  78  будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра —  0,  это значит, что частное будет состоять из  2  цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз  12  содержится в числе  78.  Для этого мы последовательно умножаем делитель на натуральные числа  1, 2, 3, …,  пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число  6,  записываем его под делитель, а из  78  (по правилам вычитания столбиком) вычитаем  72  (12 · 6 = 72).  После того, как мы вычли  72  из  78,  получился остаток  6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше

К получившемуся остатку —  6,  сносим следующую цифру делимого —  0.  В результате, получилось неполное делимое —  60.  Определяем, сколько раз  12  содержится в числе  60.  Получаем число  5,  записываем его в частное после цифры  6,  а из  60  вычитаем  60  (12 · 5 = 60).  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит  780  разделилось на  12  нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить  9027  на  9.

Определяем неполное делимое — это число  9.  Записываем в частное  1  и из  9  вычитаем  9.  В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого —  0.  Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль  (0 : 9 = 0)  и в промежуточных вычислениях из  0  вычитаем  0.  Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого —  2.  В промежуточных вычислениях вышло так, что неполное делимое  (2)  меньше, чем делитель  (9).  В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз  9  содержится в числе  27.  Получаем число  3,  записываем его в частное, а из  27  вычитаем  27.  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число  9027  разделилось на  9  нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить  3000  на  6.

Определяем неполное делимое — это число  30.  Записываем в частное  5  и из  30  вычитаем  30.  В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого —  0.  Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из  0  вычитаем  0:

Сносим следующую цифру делимого —  0.  Записываем в частное ещё один нуль и в промежуточных вычислениях из  0  вычитаем  0.  Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток —  0.  Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит  3000  разделилось на  6  нацело:

3000 : 6 = 500.

Признаки делимости величин

Перед использованием признаков делимости чисел нужно понимать, что величины классифицируются на простые и составные. Первые делятся только на 1 и эквивалентное себе значение. Вторые могут содержать нескольких множителей. В последнем случае и необходимо использовать правила деления.

Следует отметить, что для удобства специалисты рекомендуют составить письменную карточку с таблицей простых величин или распечатать ее при помощи принтера, предварительно загрузив из интернета. Правила делимости многозначного на однозначное число имеют следующий вид (делители соответствуют порядковому номеру списка):

Любое значение, т. е. 34/1=34.
Величина, заканчивающаяся четной цифрой.
Сумма цифр разрядной сетки должна делиться на тройку.
Сумма двух последних элементов делится на четверку.
Величина заканчивается на ноль или пятерку.
Сумма цифр делится на тройку, а также число является четным.
Число разбивается на разряды по три элемента (без последних), которые суммируются между собой. Она должна делиться на 7. Если величина имеет небольшое количество знаков (двузначная, трехзначная, четырехзначная или пятизначная), то нужно взять числа без последнего компонента разрядной сетки. Затем от них отнять удвоенное значение разряда единиц. Результат разности должен делиться на 7. Например, 259/7 -> 25−2*9=25−18=7 (делится).
Если выполняется условие для 2 и 4 одновременно.
Сумма компонентов разрядной сетки делится на девятку.
Величина заканчивается 0.

Следует отметить, что реализация правила деления величины 45134412 на семерку выполняется следующим образом: | 45 | 134 | 412 =9+8+7=24 — не делится на 7. Применить способ для малого количества разрядов не получится, поскольку на вычисления будет затрачено много времени.

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг. Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг. Ставим точку под делителем.

5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными (многозначными) числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

2.4.1 Деление окружности на равные части и построение правильных вписанных многоугольников

Для
деления окружности пополам достаточно
провести любой еедиаметр. Два
взаимно
перпендикулярных диаметра разделят
окружность на четыре равные
части
(рисунок 28, а).Разделив
каждую четвертую часть пополам, получают
восьмые части, а при
дальнейшем делении – шестнадцатые,
тридцать вторые части и т. д. (рисунок
28, б).Если
соединить прямымиточки
деления, то можно получить стороны
правильного вписанного квадрата(а₄),
восьмиугольника (а₈)
и т. д.
(рисунок 28, в).

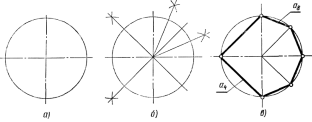
Рисунок
28

Деление
окружности на 3, 6, 12 и т, д. равных частей,
а также построение соответствующих
правильных вписанных многоугольников
осуществляют следующим образом. В
окружности проводят два взаимно
перпендикулярных диаметра1–2 и3–4 (рисунок 29 а). Из точек1 и2 как из центров описывают дуги
радиусом окружностиRдо пересечения с ней в точкахА,
В, С иD. ТочкиA,B,1, С, Dи2делят окружность на шесть
равных частей. Эти же точки, взятые через
одну, разделят окружность на три равные
части (рисунок 29, б). Для деления окружности
на 12 равных частей описывают еще две
дуги радиусом окружности из точек3
и4 (рисунок 29, в).

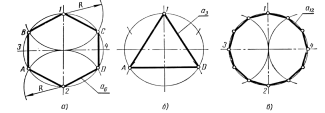
а
б
в

Рисунок
29

Построить
правильные вписанные треугольник,
шестиугольник и т. д. можно также с
помощью линейки и угольника в 30 и 60°. На
рисунке 30 приведено подобное построение
для вписанного треугольника.

Рисунок
30

Деление
окружности на семь равных частейи построение правильного вписанного
семиугольника (рисунок 31) выполняют с
помощью половины стороны вписанного
треугольника, приблизительно равной
стороне вписанного семиугольника.

Рисунок
31

Для
деления окружности на пять или десятьравных частейпроводят два
взаимно перпендикулярных диаметра
(рисунок 32, а). РадиусOAделят пополам и, получив точкуВ,
описывают из нее дугу радиусомR=BCдо пересечения ее в точкеDс горизонтальным диаметром.
Расстояние между точкамиCиDравно
длине стороны правильного вписанного
пятиугольника (а₅),
а отрезокODравен длине стороны правильного
вписанного десятиугольника (а₁₀).
Деление окружности на пять и десять
равных частей, а также построение
вписанных правильных пятиугольника и
десятиугольника показаны на рисунке
32, б. Примером использования деления
окружности на пять частей является
пятиконечная звезда (рисунок 32, в).

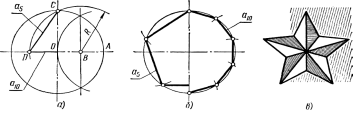
а
б
в

Рисунок
32

На
рисунке 33 приведен общий способ
приближенного деления окружности на
равные части. Пусть требуется
разделить окружность на девять равных
частей. В окружности проводят два взаимно
перпендикулярных диаметра и вертикальный
диаметрABделят
на девять равных частей с помощью
вспомогательной прямой (рисунок 33, а).
Из точкиBописывают
дугу радиусомR=AB, и
на пересечении ее с продолжением
горизонтального диаметра получают
точкиСиD.
Из точекCиDчерез
четные или нечетные точки деления
диаметраABпроводят лучи. Точки пересечения
лучей с окружностью разделят ее на
девять равных частей (рисунок 33, б).

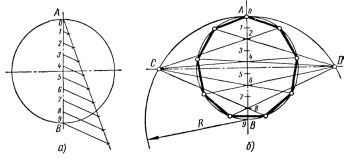
Рисунок
33

При
построении необходимо учитывать, что
такой способ деления окружности на
равные части требует особенно большой
точности выполнения всех операций.

Обучение делению многочленов

Деление многочленов

Детям нужно рассказать тонкости деления данного формата:

• По итогу деления может быть остаток, так же он может отсутствовать.
• Чтобы совершать вычитание, нужно дополнять в многочлен недостающей степенью функции, умноженной на 0.
• Делайте преобразование многочлена с помощью выделения повторяющихся многочленов или двучленов. При сокращении получится ответ без остатка.

Рекомендации для легкого обучения ребенка

Также важно пробудить интерес к предмету у ребенка. Этому способствуют аналоги математических игр в процессе игры

Наблюдение за природой тоже можно преобразовать в увлекательную математику.

Родителям нужно тренировать наблюдательность детей. Это ключ к пониманию математики и других предметов.

Можно обзавестись полезными таблицами умножения и деления. Плакаты можно повесить в комнате ребенка. Тогда он может в любой момент ими воспользоваться и справиться с задачами.

Деление в столбик

Как научиться ребенку делить числа в столбик

9 Общий Балл

Научить ребенка делению чисел

Достоверность информации

9.5

Актуальность информации

8

Раскрытие темы

9

Доступность применения

9.5

Легкость запоминания

7.5

Плюсы

• При регулярных занятиях, каждый ребенок поймет даже самый сложный материал
• Деление входит в школьную программу
• Ребенка можно учить в игровой форме

Минусы

• Некоторым детям сложно воспринимать и запоминать информацию математического характера
• Для успешного изучения необходимо повторять материал

Алгоритм деления столбиком пошагово!

После того, как вы записали делимое и делитель по выше описанному правилу, считаем сколько цифр имеет делитель. В скрине ниже — делитель состоит из одной цифры — 4.

Смотрим на делимое(число, которое будем делить), а точнее на первую цифру слева(2) и сравниваем её с делимым(4). Очевидно, что 4 > 2 из чего получается, что при делении 2 на 4 мы целых не получим — это нам не подходит, переходим ск следующему пункту.

Далее смотрим на число, которое составляет две цифры слева — 23. Понятно, что 23 > 4. Если мы разделим 23 на 4, то получим 5 и 3 в остатке. Скобки применены, чтобы вы понимали, какое действие будет выполняться первым.

23 : 4 = (4 * 5) + 3

5 — записываем под горизонтальной линией, под делителем.

20 — результат умножения делителя и частного 4 * 5 = 20, записываем под делимым 23.

Отнимаем от делимого(23), полученный результат(20) , 23 — 20 = 3.

3 — получился остаток, который меньше 4.

Если вы еще не изучали десятичные дроби. То здесь мы останавливаемся.

Итого :

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным.  Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Решаем реальные примеры

Задача № 1

Теперь выполним те же самые шаги, но не с числами, а с многочленами. Для примера возьмем такое:

\

Обратите внимание, если при делении чисел друг на друга мы подразумевали, что делимое всегда больше делителя, то в случае деления полиномов уголком, необходимо, чтобы степень делимого была больше, чем делителя. В нашем случае все в порядке — мы работаем с конструкциями второй и первой степени

Итак, первый шаг: сравниваем первые элементы. Вопрос: на что нужно домножить $x$, чтобы получилось ${{x}^{2}}$? Очевидно, что на еще один $x$. Умножаем $x+5$ на только что найденное число $x$. У нас есть ${{x}^{2}}+5$, которое вычитаем из делимого. Остается $3x$. Теперь сносим следующее слагаемое — пятнадцать. Снова посмотрим на первые элементы: $3x$ и $x$. На что следует домножить $x$, чтобы вышло$3x$? Очевидно, что на три. Домножаем почленно $x+5$ на три. Когда мы вычтем, то получим ноль.

Как видите, вся операция деления уголком свелась к сравнению старших коэффициентов при делимом и делителе. Это даже проще, чем когда вы делите числа. Тут не требуется выделять какое-то количество разрядов — мы просто на каждом шаге сравниваем старшие элементы. Вот и весь алгоритм.

Задача № 2

Давайте попробуем еще:

\

Первый шаг: посмотрим на старшие коэффициенты. На сколько нужно домножить $x$, чтобы записать${{x}^{2}}$? Домножаем почленно

Обратите внимание, при вычитании у нас получится именно $2x$, потому что

\

Сносим -2 и снова сравним первый полученный коэффициент со старшим элементом делителя. Итого у нас вышел «красивый» ответ.

Переходим ко второму примеру:

\

В этот раз в качестве делимого выступает полином третьей степени. Сравним между собой первые элементы. Для того чтобы получилось ${{x}^{3}}$, необходимо $x$ домножить на ${{x}^{2}}$. После вычитания сносим $9x$. Домножаем делитель на $-x$ и вычитаем. В итоге наше выражение полностью разделилось. Записываем ответ.

Задача № 3

Переходим к последней задаче:

\

Сравниваем ${{x}^{3}}$ и $x$. Очевидно, нужно домножить на ${{x}^{2}}$. В итоге мы видим, что мы получили очень «красивый» ответ. Записываем его.

Вот и весь алгоритм. Ключевых моментов здесь два:

1. Всегда сравнивайте первую степень делимого и делителя — повторяем это на каждом шаге;
2. Если в исходном выражении пропущены какие-либо степени, при делении уголком их обязательно следует добавить, но с нулевыми коэффициентами, иначе ответ будет неправильным.

Больше никаких премудростей и хитростей в таком делении нет.

Обучение делению столбиком в уме

В уме дети считают тоже столбиком. Это удобно и знакомо. У детей развито воображение, поэтому они смогут быстро освоить технику. Приступать к обучению деления столбиком в уме нужно тогда, когда ребенок без труда справляется с делением в тетради. Обучение:

• Расскажите школьнику о том, что делить столбиком можно не только в тетради, но и в уме.
• Объясните ученику о том, что частное можно разложить на составляющие.
• Значение 3647необходимо поделить на 7. Нужно показать частное как сумму чисел 3500 и 147. Значение 3500 самое оптимальное, так как его можно поделить на 7, не имея остатка. В результате деления 3500 на 7 получается 500, а при делении 147 на 7 получается 21. Числа 500 и 21 нужно сложить, в результате получится 521. Данное число является ответом в примере деления 3647 на 7.

Ребенок не сразу может освоить эту технику деления. Все зависит от родителей. Их задача заключается в помощи ребенку без давления.

Делим десятичные дроби на 1000, 100, 10: как это сделать правильно?

Исходя из имеющихся и известных правил деления так называемых «обыкновенных дробей», деление на числа с нулями равносильно умножению. Необходимо перенести запятую на нужное количество цифр. Если значений не хватает, нули просто добавляются. Это же происходит с бесконечными десятичными дробями.

Поэтому, чтобы верно произвести действие деления десятичной дроби на числа с нулями, нужно перенести запятую на столько цифр, сколько нулей стоит после единицы в делителе: если это число 10 – то нуль один, если 100 – то два. И так далее.

Делим десятичные дроби на 1000, 100, 10

Примеры с бесконечными дробями решаются также:

Делим десятичные дроби на 1000, 100, 10

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий при делении на двузначные числа. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.

2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.

3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.
После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка.

4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет:

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.